CBSE Class 9 Science Chapter 11 Work and Energy Notes, Explanation with Video and Question Answers
Work and Energy Class 9 – CBSE Class 9 Science Chapter 11 Work and Energy Notes and Complete explanation of the chapter. Topics covered in the lesson are Introduction to work, Definition of work, Expressions to calculate work, Units of work, Types of work, Introduction of Energy, Law of conservation of energy, Types of energy, Example of conservation of energy, Mechanical energy: potential and kinetic energy, Power and units, Derive an expression for Kinetic energy. Given here is the complete explanation of the chapter, along with all the important questions and NCERT solutions to book questions have also been provided for the ease of students. Also, Take a free Online MCQ Test For Class 9.
Class 9 Science Chapter 11 – Work and Energy
Part -1 Work
Topics to be covered
- See Video Explanation Chapter 11 – Work and Energy Part 1
- Introduction to work
- Definition of work
- Expressions to calculate work
- Units of work
- Types of work
Work and Energy Video Explanation Part 1
Click Here for Work and Energy MCQs
Introduction to work
As you all know, in daily routine we do a lot of work like cooking, bathing, studying, carrying bag and lots more. But do you know that actually all of these do not fall in the category of work but are activities. In this chapter we will try to learn a lot about work.
Work is said to be done only when applied force produces motion. This means that for work to be done, one needs to apply force and motion has to be produced in a body.
For example : While we are studying, we are using our intelligence but neither we are applying motion nor motion is caused. So, this doesn’t fall in the category of work. Likewise, if we are pushing a wall, we are applying force (that is the reason our hands start paining after sometime), but the motion is not produced in the body. So, again, no work is done. Now, if you are playing with your friend and you push him and he falls. This comes in the category of work because in this, force is also applied while pushing and motion is also produced (as he falls).
Top
Definition of work
Work can be defined as: Work is done when force is applied which causes displacement in the body in its own direction.
Factors on which force depends
W ∝ F
W ∝ S (Displacement).
Or W ∝ F.S
W = k .F. S
Where k is constant and its value is = 1.
Work is a scalar quantity as it specifies only magnitude not direction.
Top
Expressions to calculate work
Expression for work done against gravity
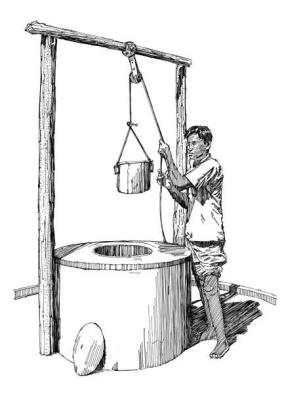
If we pick or drop anything, it falls to the ground. Like a child drops the ball on the ground or a person lifts the bucket from well. So, in this case, work is done in response to gravity. So, in this case the expression to calculate work is given by:
W = m*g*h
This is obtained by substituting the value of force as mass and acceleration and distance as height. Therefore, the relation becomes W= mgh (where m=mass, g=acceleration due to gravity and h=height to which the body is raised or dropped).
Expression for work done when the force makes an angle with the direction of displacement

Suppose the child is playing with a toy where he is pulling it with the help of a string. Now, in this case, the force is applied on a string and displacement is caused in it due to force applied.
In this case, we have to consider an angle also which force makes with the ground or with the direction of displacement, which is usually taken in terms of theta. So, expression for work becomes:
W=FScos θ
Now, the value of work depends upon the magnitude of angle. Accordingly, it can be maximum or minimum. Like if angle is 0⁰ then:
W=FScos0⁰
Therefore, W=FS (because cos 0⁰ = 1)
Likewise, if angle is 90⁰ then, the work done is :
W=FScos90⁰
Therefore, W =0 (because cos 90⁰ = 0)
Please note:
- work done is maximum, when θ = 0⁰
- Work done is minimum, when θ =90⁰
Unit of work
As we know, every physical quantity is measured in specific kind of unit. Likewise, the S.I. unit of work is Joule.
We know, W = F .S
So, 1 joule = 1 Newton x 1 meter or 1 nm
We can define 1Joule as: “Work is said to be 1 joule when 1 Newton of force acts on a body and causes displacement of 1m in its own direction”.
The bigger units of work are gigajoule, megajoule, etc.
Let us see the relation between joule, megajoule and kilojoule
1 GJ = 109 J
1MJ = 106 J
Types of work

Now, if we focus on its types, we have three different kinds of work depending upon the direction of displacement in accordance with force.
As you all have observed that if we kick a ball, it goes in the direction in which it is being kicked.
Similarly, if you notice, while walking on the floor, one foot pushes the ground backward and the other moves forward. This is how we move. But you are familiar that for walking, running, etc we need to apply force. The reason is that the ground doesn’t allow us to move because of the frictional force (opposing force that comes into play when two bodies are rubbed with each other).
Similarly, if the coolie carries the load on his head and moves on the platform. In this case also, force is applied but it is at a certain angle with the direction of displacement (angle is 90⁰).
Accordingly, we have three different kinds of work:

- Positive work
- Negative work
- Zero work.
Positive work: when force applied causes displacement of body in its own direction. Like pushing of door, kicking football, etc.
Negative work: when applied force causes displacement of body in its opposite direction. Example : In case of friction.
W = – F x S (negative work is done).
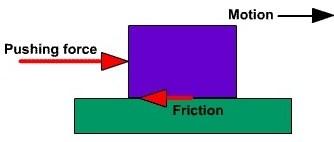
Zero work: It is done when force acts at a right angle to the direction of displacement.
That is: W=FScos θ
W=0
Now if you wonder that work done is zero when a person carrying suitcase vertically in hand walks in a horizontal direction. This is because the angle between the direction of force and the direction of displacement is 90o.
We know:
W = F. S cos θ
W= F .S cos 90o
W=F.S.0
W = 0
Similarly, for a body moving in a circular path, the work done is zero due to similar reasons.
Work and Energy Part 2 Energy
Topics to be covered:
- See Video Explanation Chapter 11 – Work and Energy Part 2
- Introduction
- Law of conservation of energy
- Types of energy
- Example of conservation of energy
- Mechanical energy: potential and kinetic energy
- Power and units
- Derive expression for Kinetic energy
- NCERT Book solutions
Work and Energy Video Explanation Part 2
Introduction
As we have already discussed that we need to do a lot of work and for doing work we need strength and that strength comes from the food we eat. For example, if you need to ride a bicycle, you need to paddle it and for paddling you need to do work and for it you need strength which comes from food.The strength here refers to energy.
So, we can define energy as: energy is the ability to do work.
- It is a scalar quantity.
- It depends upon work therefore. its unit is the same as that of work that is Joule.
Types of Energy
Energy is of different types like a machine produces mechanical energy, the heating devices produce heat energy, bulb, etc produce light energy. So, we actually come across different forms of energy. The common form that we are going to consider here is Mechanical Energy. Let us check it out.
Mechanical energy: It is the energy possessed by a body due to its position or motion.
Suppose you notice a book lying on a table. Do you think it possesses any kind of energy?
Yes, it does and that is the energy due to its position, called potential energy.
Likewise, if we notice a girl riding a bicycle or a car moving on the road, they all are moving so, they possess energy due to motion that is kinetic energy.
Top
Mechanical energy: potential and kinetic energy
Types of mechanical energy
- Potential energy
- Kinetic energy
We can define both as:
1. Potential energy is the energy possessed by a body by virtue of its position.
It is given by the following relation:
P.E. = m g h
Please note: All bodies or objects possess potential energy due to their position.
2. Kinetic energy is the energy possessed by a body by virtue of its motion.
Example: A speeding train, flowing water, etc.
Derive expression for kinetic energy

Law of conservation of energy
According to it, Energy can’t be created nor be destroyed but can be converted from one form to another, but the total energy of a system remains constant.
Suppose a ball is lying at a height. We know that due to position, it possesses potential energy. Now, due to any reason, it falls down, so, its potential energy gets converted to kinetic energy. It has been observed that the total energy remains the same only the form of energy changes.
Explanation – A theoretical example to illustrate the law of conservation of energy
Consider a body of mass m at a right of h, held by a person. Let the body be released such that it falls freely under the acceleration due to gravity g. Let us consider the total energy possessed by the body at the height h from the ground level and at the ground level. Let v be the final velocity of the body on reaching the ground level.
Case (i) when the body is at a height of h from the ground level.
As the body is stationary, its velocity is zero.
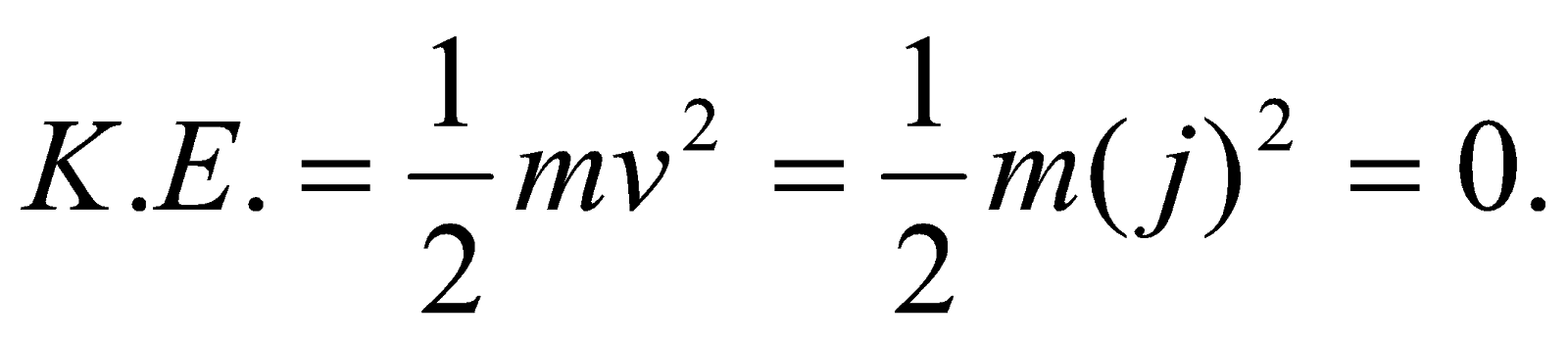
P.E. = mgh
:. Total energy of the body = P.E. + K.E. = mgh + 0 = mgh
Case (ii) When the body just reaches ground level and its height is zero.
Let us calculate the velocity of the freely falling body at ground level.
V2 = u2 + 2gh
As initially the body is at rest, therefore u2 = 0
:. V2 = 2gh
:.
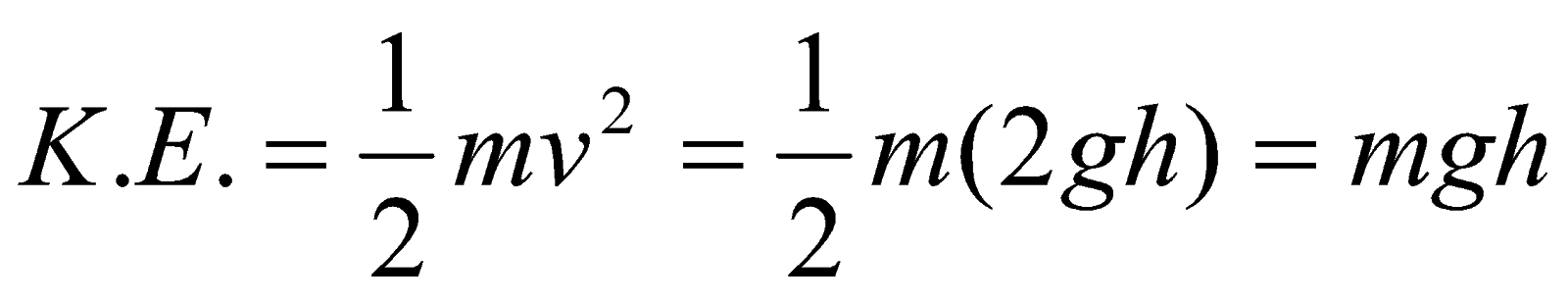
P.E. = mgh = m x g x 0 = 0
:. Total energy of the body = P.E. + K.E. = 0 + mgh = mgh.
As, the total energy of the body remains the same, the law of conservation of energy stands proved. Only energy changes its form i.e. from potential energy to kinetic energy or vice versa.
Example of conservation of energy
Examples of transformation of energy are as follows-
1. When hands are rubbed, the mechanical energy of hands changes into heat energy due to friction.
2. When two stones are struck, the mechanical energy changes into heat energy and sound energy, due to friction.
3. When the blade of a knife is placed against the rotating grinding stone, the mechanical energy change into heat, light and sound energies.
4. When the brakes are applied on any moving vehicle, the mechanical energy changes into heat energy as the brakes rub against the moving wheels.
5. When we wind a watch, the mechanical energy of hands change into potential energy of the spring. When the spring unwinds, the potential energy changes into kinetic energy and drives the hands of the clock.
6. When an arrow is stretched in a bow the mechanical energy changes into potential energy. On releasing the string of the bow, the potential energy changes into kinetic energy of the arrow.
7. Water stored in hydroelectric dams has potential energy. When this water is released, the potential energy changes into kinetic energy of the flowing water. The kinetic energy of the flowing water turns the blades of a turbine and drives the dynamo. The dynamo then produces electrical energy.
8. When a torch is switched on, the chemical energy of the cell changes into electrical energy, The electrical energy, on passing through the filament of a bulb, changes into heat energy and light energy.
9. In an electromagnet, electrical energy changes into magnetic energy.
10. The electrical energy, on flowing through the coils of an electric motor or an electric fan, changes into mechanical energy. It partly changes into heat energy and hence, heats the coils.
11. In microphone, the sound energy changes into electrical energy.
12. Electrical energy, on flowing through the speaker of an audio system, changes into sound energy.
13. In electric heaters, electric ovens and geysers, the electrical energy changes into heat energy.
14. In a locomotive, the chemical energy of coal changes into heat energy. The heat energy then changes into kinetic energy of steam which drives the locomotive.
15. In an electric generator, the mechanical energy changes into electrical energy.
16. In a photovoltaic cell, the light energy changes into electrical energy.
17. In television the electrical energy changes into light energy and sound energy.
18. On burning the fuels, their chemical energy changes into heat energy and light energy.
19. When a match stick is rubbed against the side of a match box, the chemical energy changes into heat energy and light energy.
20. When a cracker is exploded, the chemical energy (stored in the chemical used in the cracker) changes into heat, light and sound energies.
21. During photosynthesis, light energy changes into chemical energy in the presence of chlorophyll.
22. During respiration the chemical energy of food changes into heat energy. It is the heat energy which keeps our bodies warm. It is also the heat energy which changes into mechanical energy during locomotion.
23. During charging of a battery the electrical energy changes into chemical energy.
24. During nuclear fission or fusion, it is the nuclear energy which ultimately changes into heat energy and light energy.
Top
Power and units
You must have noticed that whenever we buy a bulb or any electrical appliance we ask for 60W, 100W etc .this reading is Power .All the electrical appliances possess certain power which actually shows how much energy it will consume in a given time.
So, Power is defined as the rate of doing work.
Or P=W/T
Power is a scalar quantity.
Unit is Watt.
1Watt= 1Joule/1second.
Power is said to be 1Watt: When 1 joule of work is done in 1 second.
Bigger units of power are:
GW= 109 watts
MW= 106 watts.
Older unit is HorsePower =746 Watts
If we need to calculate electric energy consumed by an electrical appliance, we can calculate by :
E= n PT
Where n specifies the same kind of appliance with same power and same working hours
Then commercial unit of energy is KWhr
You must have seen your home electricity bill, and the bill that we get is like 45 units, 100 units so on. Those units are actually KWhr
1KWhr= 1 unit
We can also relate kW hr with joule as follows-
1 kWhr= 3.6 x 106 J or 3.6 MJ
1 kWhr = 1 unit of electricity.
Top
Work and Energy Question Answers
Q1. Why work done is zero when person carrying suitcase vertically in hand walks in horizontal direction?
Ans: The Angle between the direction of force & direction of displacement is 90o.
We know
= f. s cos θ
= f. s cos 90o
= f. S.0
W = 0.
Q2. What is the magnitude of work when man is pushing a wall?
Ans.: The work done is zero in this case because in this case the displacement is zero. For the work to occur, the two necessary conditions must be satisfied that is:
- Force must be applied
- Displacement must be caused.
Q3. A force of 7 N acts on the object. The displacement is 8m in the direction of force. Let us take that the force acts on the object through the displacement. What is the work done in this case?
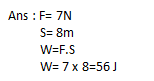
Q4. A pair of bullock exerts a force of 140N on a plough. The field being ploughed is 15m long. How much work is done in ploughing the length of field?

Q5. Please list out whether work is done or not in the following-
Suma is swimming in a pond
A donkey is carrying load on his back
A wind mill is lifting water from a well
A green plant carrying out photosynthesis
An engine is pulling a train
Food grains getting dried in the sun
A sail boat is moving due to wind energy
A.
A. Suma is swimming in a pond (work done)
A donkey is carrying load on his back (work not done)
A wind mill is lifting water from a well (work done)
A green plant carrying out photosynthesis (work not done)
An engine is pulling a train (work done)
Food grains getting dried in the sun (work not done)
A sail boat is moving due to wind energy (work done)
Q 6: Write the expression for the work done when force is acting on an object in the direction of displacement?
Ans: W= F.S
Q7: Define 1 J of work?
Ans: When force of 1 N acts on a body causing displacement of 1 m.
Q 8: An object thrown to certain angle to the ground moves in a curved path and falls back to the ground .The initial and final points of the path of object lie on the same horizontal line. What is the work done by the force of gravity on the object?
Ans: Zero
Q9: Certain force acting on a 20Kg mass changes its velocity from 5m/sec to 2m/sec .Calculate the work done?
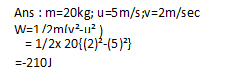
p>
Q10. A mass of 10 kg is at a point A on table .It is moved to a point B. If line joining A and B is horizontal, what is the work done on the object by gravitational force .Explain your answer?
Ans: Force is being applied in vertical direction and displacement is in horizontal direction. There is no displacement in direction of force applied therefore, work done is zero.
Q11.What is the work done when satellite revolves around the planet? Justify your answer
Ans: Zero, The angle between the direction of force & direction of displacement is 90o.
We know
= f. s cos θ
= f. s cos 90o
= f. S.0
W = 0.Similarly, for body moving in a circular path.
Q12 Relate GW & MW with watt?
Ans : 109 watt and 106 watts
Q13. What is the commercial unit of Energy?
Ans: KWhr
Q14. Relate KWhr with joule?
Ans: 1 KWhr = 3.6 x 106 J or 3.6 MJ
1 KWhr = 1 unit of electricity.
Q15. A lamp consumes 1000J of electric energy in 10 seconds. Calculate its power?
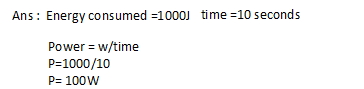
Q16. Define Average Power?
Ans: It is the ratio of total work done to the total time taken.
Q17. A certain household has consumed 250 units of energy during a month. How much energy is this in joules?
Ans: Units consumed = 250=250KWhr ( 30 days )
The energy consumed in joules = 250 x 3.6 x 106 J=9 x 108J
Q18. An electric heater is rated at 1500W. How much energy is consumed in 10 hours?
Ans: P=1500 W
T = 10 hrs
E= n PT
E =1 x 1500 x 10=15000Wh
Q19. Find the energy in kilowatt hour consumed in 10 hours by four devices of power 500 watt each?

Q20. What is the kinetic energy of an object?
Ans: It is the energy possessed by a body by virtue of its motion.
Q21. Write an expression for kinetic energy?
Ans: K.E = 1/2mv²
Q22. The kinetic energy of an object of mass m moving with velocity of 5m/sec is 25J.what will be its kinetic energy when the velocity is doubled ?what will be the kinetic energy if the velocity is increased three times ?
Ans: K.E=1/2 mv²
25=1/2m (5)²
When velocity is doubled: v=2×5=10m/sec
Then K.E=1/2 x 2 x (10)2=100J
When velocity is increased three times, we get
K.E=1/2 x 2 x (15)2=225J
Q23.A battery lights a bulb. What is the energy conversion?
Ans: Electric energy is converted into heat energy.
Q24.The potential energy of freely falling object decreases progressively .does this violate the law of conservation of energy?
Ans: As potential energy decreases as body falls and kinetic energy increases .Therefore, it doesn’t violate .
Q25. What is the energy transformation while riding a bicycle?
Ans: chemical energy of food – mechanical energy, sound and heat energy .
Q26.Can there is displacement in object in absence of external force?
Ans: Yes, if the body is initially in uniform motion, it will continue to move uniformly in a straight line.
Q27.A person holds bundle of hay over his head for 30 minutes and gets tired. Has he done some work or not? Justify.
Ans: Since there is no displacement of hay in the direction of force applied, therefore, work done by hay is indeed zero.
Q28. An object of mass m is moving with velocity V .how much work is done on the object in order to bring it to rest?
Ans:

1 MW = 106 watts
Q29. A freely falling object eventually stops on reaching the ground. What happens to its kinetic energy?
Ans: Its kinetic energy is converted into heat and sound energy.
Q30. Calculate the work required to be done to stop a car of 1500kg moving with velocity 60km/hr?
Ans: u=60km/hr=60×5/18=50/3m/sec
Kinetic energy = 1/21500x (50/3)²
=208333J
Q31. The potential energy of freely falling object decreases progressively .does this violate the law of conservation of energy?
Ans: As potential energy decreases as body falls and kinetic energy increases .Therefore, it doesn’t violate.
Q32. The potential energy of freely falling object decreases progressively. Does this violate the law of conservation of energy?
Ans: As potential energy decreases as body falls and kinetic energy increases. Therefore, it doesn’t violate the law of conservation of energy.
Top
